למדנו את האלגוריתם של אוקלידס למציאת מחלק משותף גדול ביותר (gcd). האלגוריתם הזה הוא עתיק, קצר, מבריק ומהיר.
נתאר את הרעיון. נניח שקימים המספרים הטבעיים הבאים:
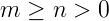
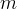 במספר
במספר
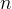 מקבלים מנה
מקבלים מנה
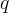 (quotient)
ושארית
(quotient)
ושארית
 (residue).
(residue).
אפשר לתאר זאת בנוסחאות:
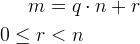
קל לראות שתי תכונות:
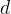 מחלק את
מחלק את
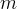 וגם את
וגם את
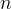 אז
הוא מחלק
גם
את
אז
הוא מחלק
גם
את
 .
.
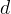 מחלק את
מחלק את
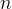 וגם את
וגם את
 אז
הוא מחלק
גם
את
אז
הוא מחלק
גם
את
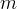 .
.
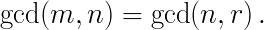
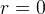 ומשתמשים בעובדה ש
ומשתמשים בעובדה ש
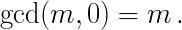
lcm.py
שמחשבת כפולה משותפת קטנה ביותר
(lcm)
כמו בתרגיל של
שעור קודם
אבל הפעם הפונקציה לחישוב המחלק המשותף הגדול ביותר מיושמת
על ידי האלגוריתם של אוקלידס.